Part -2:本文说明
本文只介绍八年级会用到的一些因式分解技巧
文章为原创,所有的公式在和Photomath中均验证过
Part -1:幂的运算
请记住以下公式:
$a^b\cdot a^c = a^{b+c}$
$\frac{a^b}{a^c} = a^{b-c}$
$(a^m)^n = a^{mn}$
$a^c\cdot b^c=(ab)^c$
$a^0 = 1(a \neq 0)$
$a^{-p}=\frac{1}{a^p}(a\neq 0)$
Part 0:什么是因式分解
因式分解是整式乘法的逆运算,举个例子:
$c(a+b) = ac + bc$
从右到左是因式分解,从左到右是整式乘法
也就是说:
因式分解是添加小括号,用乘法表示一个代数式
整式乘法是去掉小括号,用加法表示一个代数式
请注意,因式分解不改变原式的值,并且倒退回去可以得到原式
Part 1:因式分解第一招——乘法分配律!
例1:对以下式子进行因式分解:
$(1) 2a + 2b$
$(2) 2a^2 + 4ab$
$(3) 2ab + 2bc + 2abc$
$(4) 2ca + 2bc^2$
首先看第一个:
我们可以发现,他正好符合$ac + bc$的形式,话不多说,直接运用:
$\text{解:}(1): 2a+2b = 2(a+b)$
再来看第二个,这个式子里边有平方,怎么办呢?
请记住:目前为止,有平方?你就拆!
第二个问题:4和2,怎么运用乘法分配律呢?
小可爱,你知道$2\times 2=4$ 吗?
$2a^2+4ab = 2a\cdot a+ 2ab \cdot 2$
提取一个$2a$,可得:$2a(a+2b)$
第三个,有的小可爱一看到就开心了,直接提取一个$2b$:$2b(a+c+ac)$
第四个,也很好做啊!提取$2c$:$2c(bc+a) $
Part 2:公式的运用
不是所有时候都可以用到乘法分配律,于是,公式出来了:
$a^2-b^2=(a+b)(a-b)$
$a^2+2ab+b^2=(a+b)^2$
$a^2-2ab+b^2=(a-b)^2$
这是你基本要记住的几个,我们来几个题:
$(1)(x-y)^2-4$
如果你敏感的话,你很快就能看出来:原式就是:
$a^2-b^2(a = x-y,b = 2)$
好的,直接用公式,也就是:
$(x-y+2)(x-y-2)$
第二个:$x^4-2x^2 y^2+y^4$
啊哈,不就是$(a-b)^2=a^2-2ab+b^2$嘛!
直接用!转换为:
$(x^2 - y^2)^2$
嘿嘿嘿嘿,别忙着做下一题,你再审视一下这个式子:
$(x^2 - y^2)^2$
你再审视一下小括号:
$x^2-y^2$
此时你一惊:艹,还有一个$a^2-b^2$!
继续分解,原式变为:
$[(x-y)(x+y)]^2$
记得前面提到的幂的运算第四条吗?反过来用,$(ab)^c=a^cb^c$
那就继续换:
$(x-y)^2(x+y)^2$
然而,在作者验证的时候,发现有的网站这么给答案:$(y-x)^2(y+x)^2$
于是插一句话:因为偶次方具有非负性,所以:$(a-b)^2=(b-a)^2$
Part 3:项太多了怎么办?分组!
分组分解法一般用于四项及以上的分组,把他们分解之后再来运用公式或者乘法分配律。
举个例子:
$xy+x+y+1$
四项,也不是公式,怎么办呢?分个组!
分组的原则一般是:**(1)有公式可以套,(2)有相同的”系数”(使用主元法)**
啊这里也没啥公式可以用,就考虑使用相同系数吧:
这里我假设把y当为未知数(这是后面会讲到的主元法)
$(x+1)y + (x+1)$
哦,可以乘法分配律了!:
$(x+1)(y+1)$
当然,分组的灵活性很大,只能自己慢慢摸索(我指的是多刷题)
Part 4:特殊二次三项式的杀手:十字相乘
十字相乘用于特殊的二次三项式,特殊在哪里呢?他要满足这个要求:
假设我们有一个二次三项式:$a+b+c$
这个时候,令$mn=c,pq=a$
我们要求:$qm+pn=b$
晕了吗?好吧,我要打120啦!
我们上一张图: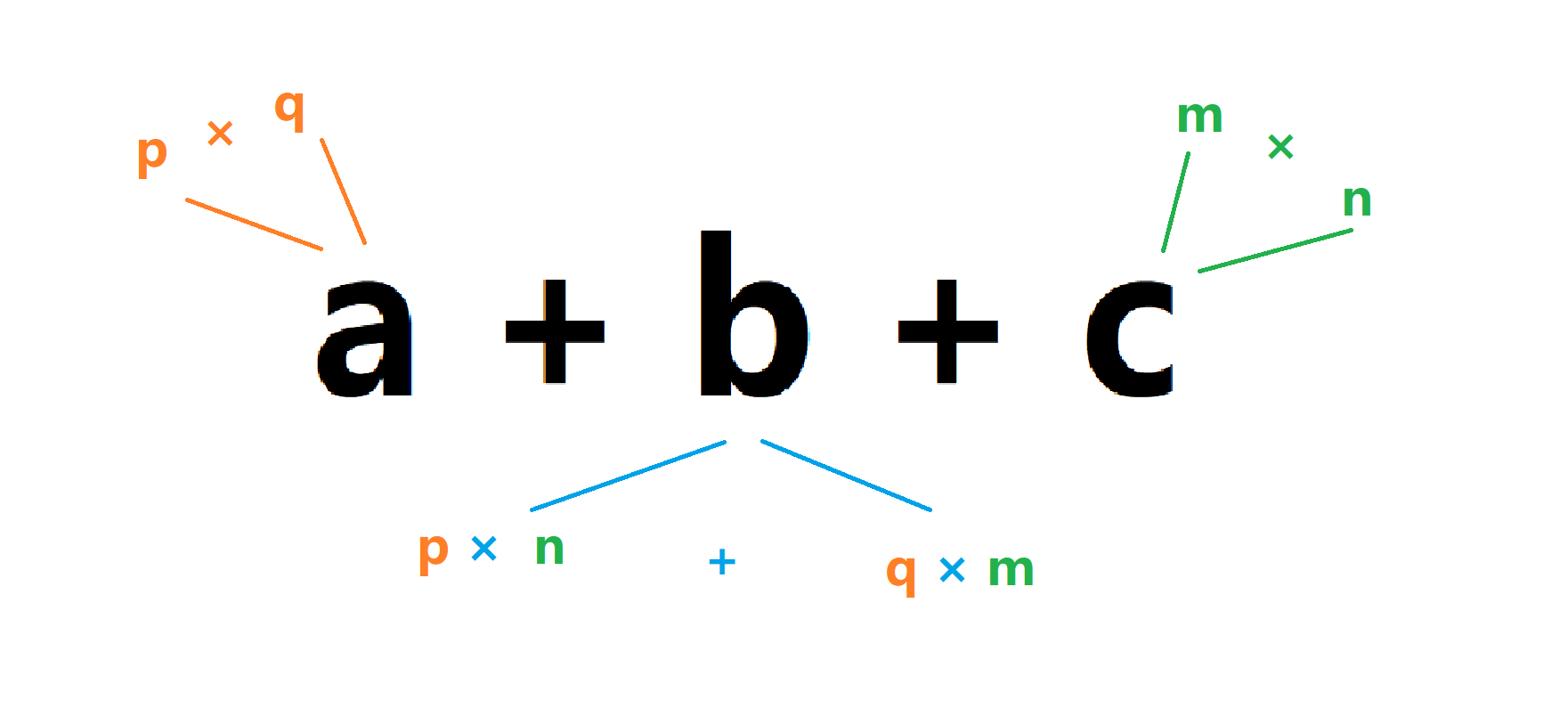
看懂了吗?他分解之后,应该是这个样子的:
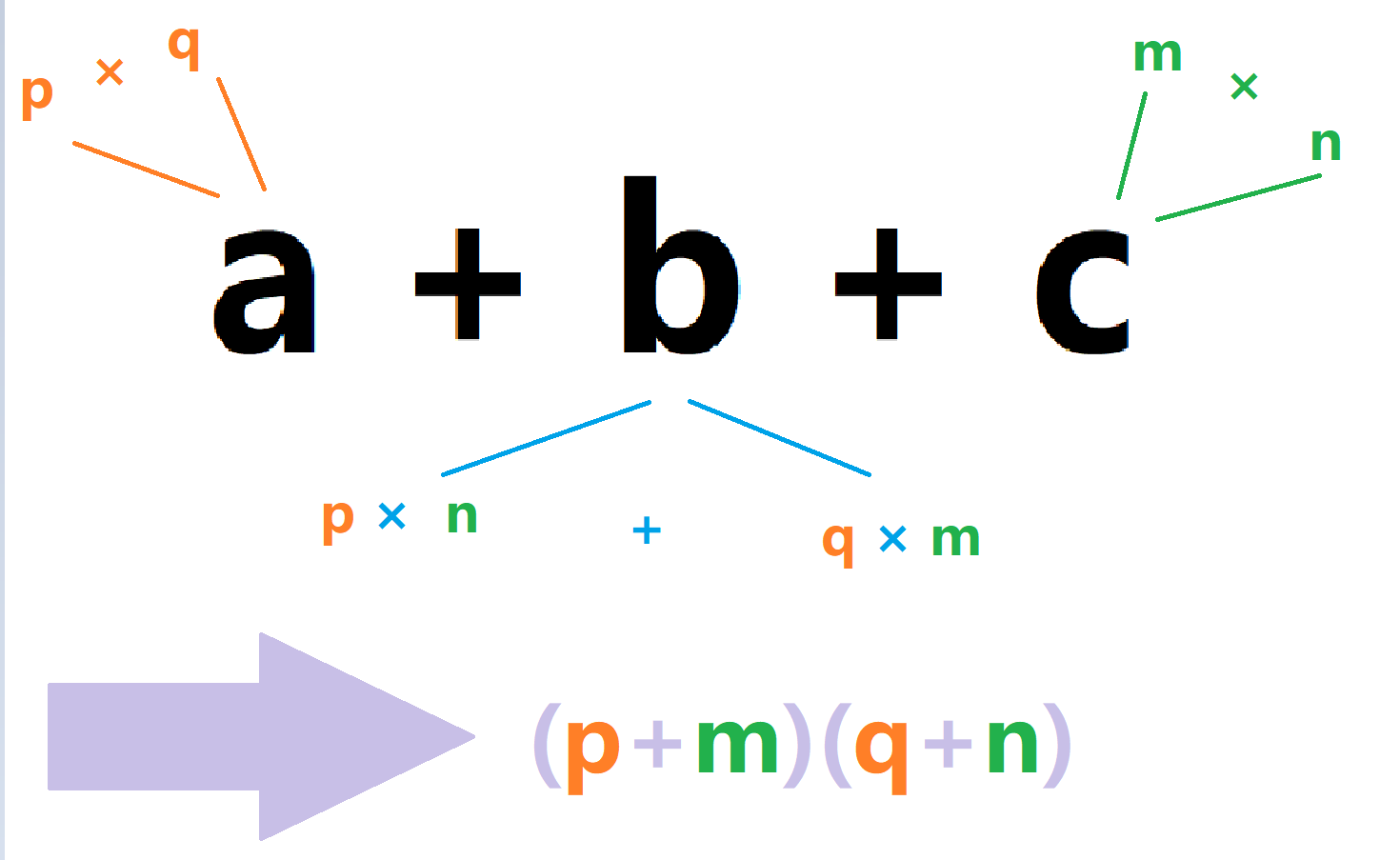
咱举个栗子:$x^2-4xy-12y^2$
我们先观察,发现:$x\cdot x = x^2,2y \cdot (-6y) = -12y^2,2y\cdot x+x \cdot (-6y) = -4xy$
好!直接分解,变为:$(x+2y)(x-6y)$
但在考试的时候,你的过程要这么写: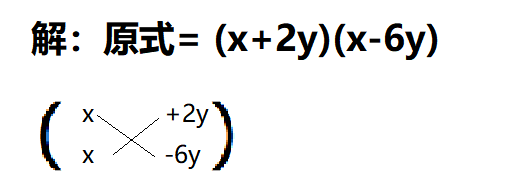
Part End:来自DBXXX大佬的友情提示: