题目大意
给定$a,b,c(0< a,b,c\leq10000)$,要求:
- 如果三条线段不能组成一个三角形,输出$\texttt{Not triangle}$;
- 如果是直角三角形,输出$\texttt{Right triangle}$;
- 如果是锐角三角形,输出$\texttt{Acute triangle}$;
- 如果是钝角三角形,输出$\texttt{Obtuse triangle}$;
- 如果是等腰三角形,输出$\texttt{Isosceles triangle}$;
- 如果是等边三角形,输出$\texttt{Equilateral triangle}$。
- 如果这个三角形符合以上多个条件,请分别输出,并用换行符隔开。
思路
首先,我们知道三角形不等式,也就是:
$$a+b> c,a+c>b,c+b>a$$
那么我们有第一个代码:
1 | if( !( (a + b > c) && (a + c > b) && (b + c > a) ))cout << "Not triangle" << endl; |
如果你知道勾股定理,也就是,对于一个直角三角形,一定有两直角边平方的和等于第三条边的平方,也就是:
$$a^2+b^2=c^2$$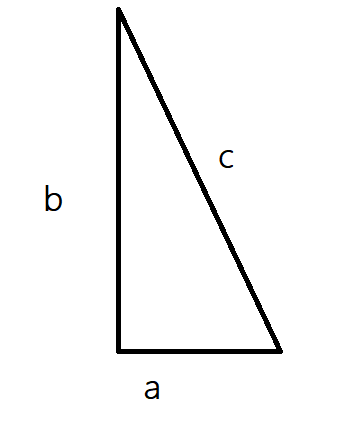
那么我们有:
1 | if(a*a+b*b==c*c) cout << "Right triangle" << endl; |
那么我们要思考,锐角三角形和钝角三角形怎么办呢?不妨我们来画个图:
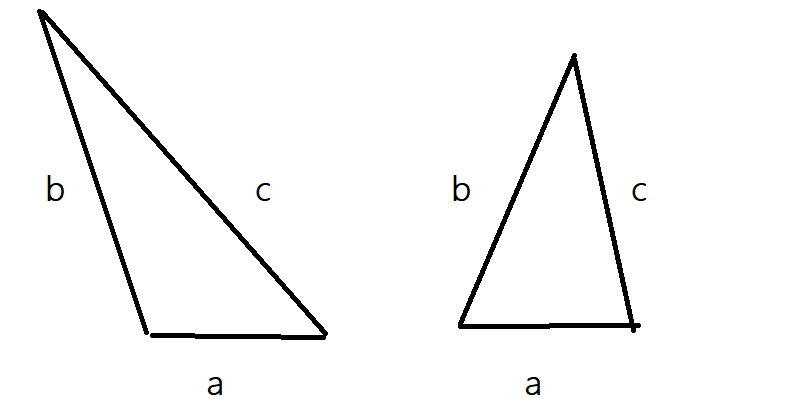
我们令$a$不变,移动$b,c$,那么你会发现:钝角三角形相当于直角三角形$b$的增长,那么一定有:$a^2+b^2>c^2$;锐角三角形相当于$b$的缩小,那么就有:$a^2+b^2<c^2$
那么我们有:
1 | if(a*a+b*b<c*c) cout << "Acute triangle" << endl; |
那等腰三角形和等边三角形就好判断了:
1 | if(a==b||a==c||b==c) cout << "Isosceles triangle" << endl; |
那么,完整代码:
1 |
|


